Оказывается нельзя. Давайте разберемся почему.
Для начала выясним, что скрывается под таким общеупотребительным определением – «система координат». Система координат – это способ задания положения точек в пространстве. Главное свойство всех систем координат – положение любой точки однозначно определяется ее координатами. Так же как по адресу можно найти лишь одно здание в пределах города.
Люди издавна измеряли все, что поддается измерению. Расстояние, скорость, время… Технологический прогресс цивилизации можно проследить по эволюции измерительных приборов: от веревки с узелками до сверхточных атомных часов. И любые измерения в пространстве немыслимы без системы координат. Самая известная из всех и широко используемая, безусловно, прямоугольная система координат.
Существуют еще полярная, сферическая и много других систем. Зачем столько? Приведу такой пример. Перед вами стоит задача получить координаты точек лежащих на окружности. Можно использовать прямоугольную систему координат и получить пары координат X и Y, поочередно измеряя положение каждой точки. Но можно перейти к полярной системе координат, однократно измерить радиус окружности R и далее измерять угол между отрезком-радиусом (называемым радиус-вектором) и одной из прямоугольных осей. Второй способ представляется более простым.
Итак, выбор конкретной системы координат зависит в первую очередь от удобства применения для поставленной задачи. А такое множество систем координат объясняется многообразием мира и широтой человеческой деятельности. Но нас это пугать не должно. Знать все придуманные человеком способы задания точек в пространстве необязательно.
Теперь от геометрии перейдем к геодезии. Геодезические системы координат имеют более широкое определение. Да, они тоже задают положение точек в пространстве, и пространством в этом случае всегда служит наша планета, но так как наша планета не шар идеально сферической формы то существует множество геодезических систем координат, а с ними и столько сложностей при переходе от одной системы к другой.
Математически точно описать фигуру Земли практически невозможно, потому что невозможно задать конечную функцию, которая представит поверхность Земли. Упрощенное представление фигуры Земли – это геоид. Фигура, которая получается, если представить, что на нашей планете нет материков и островов, а есть лишь бесконечный мировой океан. Поверхность этого океана и определит поверхность геоида. Основное свойство геоида в том, что вектор силы тяжести в любой точке геоида перпендикулярен его поверхности (составляет с поверхностью прямой угол). Если мы привяжем к нитке грузик, то нить укажет нам направление точно в центр масс Земли, а для геоида еще и будет перпендикулярна его поверхности. Фигура геоида постоянно уточняется и усложняется. Но даже упрощенный и неточный геоид для практического применения оказался слишком сложным.
С давних времен Земля расчерчена меридианами и параллелями и координаты на ее поверхности определяются двумя углами – широтой и долготой. Широта отсчитывается от экватора к северному полюсу и к южному (северный полюс это 90° северной широты, а южный - 90° южной широты). Долгота же отсчитывается от нулевого меридиана на запад и восток. Нулевой меридиан проходит через Гринвическую обсерваторию, которая находится в Великобритании. Почему, например, не через Елисейские поля в Париже? Просто так сложилось исторически, хотя претендентов провести нулевой меридиан через задний дворик родного университета или обсерватории было достаточно.
Я описал сферическую систему координат. До развития астрономии она показывала положение точки на шаре, затем оказалось, что шар этот сплюснут у полюсов и является эллипсоидом. Эллипсоиды и по сей день используются для задания формы Земли. Они представляют слишком упрощенную модель, но, вспомним, что когда-то Землю вообще считали плоской.
Почему я говорю здесь о множестве эллипсоидов? Неужели нельзя обойтись одним?
Давайте проведем мысленный эксперимент. Возьмем кусочек пластилина и попытаемся вылепить из него сферу, размером с шарик для пинг-понга. Теперь возьмем шарик для пинг-понга и поставим рядом с нашей лепкой. Пластиковый шарик это математическая модель пластилинового шарика. Предположим, что мы поместили шарик для пинг-понга внутри пластилинового и можем менять его радиус и положение относительно центра. Теперь если нам нужно максимально точно повторить какой-то участок пластилиновой поверхности мы можем подогнать нашу математическую модель. Но точное соответствие одному участку поверхности может вылиться большим несовпадением в другом месте! Поэтому не существует одного универсального эллипсоида, который точно бы повторял поверхность Земли во всех точках.
С наступлением космической эры фигура Земли была измерена максимально точно, и на основании данных измерений получили параметры общеземного эллипсоида, среднеквадратичное отклонение поверхности (погрешность) от истинного значения (от наиболее точного геоида) для всей планеты у которого минимально. Самый популярный в наши дни эллипсоид – WGS84 , который представляет собой уточненный эллипсоид GRS 80. На нем основана общемировая геодезическая система координат, WGS 84. Она известна, в первую очередь, благодаря широкому распространению спутниковой навигации (GPS), использующей эту систему. WGS 84 – это геоцентрическая система координат, то есть начало отсчета для нее – центр Земли. Координаты задаются в градусах, как широта и долгота, соответственно от экватора и Гринвича. Но как мы уже должны понимать эти углы измеряются на эллипсоиде, принятом за основу, а это означает, что, используя другой эллипсоид, мы получим другие координаты ТОЙ ЖЕ точки. Так что, если вы имеете географические координаты, сразу поинтересуйтесь, на каком эллипсоиде они измерены.
На территории СССР использовался другой эллипсоид – эллипсоид Крассовского. Его параметры были получены в 1940 году методом высокоточных геодезических измерений. Так как этот эллипсоид изначально предназначался для государственной системы координат, он довольно точно описывает поверхность планеты для всей территории бывшего СССР и непригоден для использования, например, в Австралии. Правда наибольшая точность достигается только для западной части России, там все-таки столица.
Важно понять одно. Сами по себе системы координат ошибку в определение положения точки в пространстве не вносят, так как величина ошибки – это всегда сравнение с эталонным значением, которого просто не существует, если использовать только одну систему координат. Ошибка возникает при переходе от одной системы к другой. Например, если просто переложить координаты точки с зллипсоида WGS 84 на эллипсоид Крассовского, то ошибка может достичь сотен метров! Какая уж здесь геодезическая точность.
Для перехода из одной системы координат к другой существует набор параметров, называемый геодезическим датумом. Строгий подход подразумевает сложную математику, но даже упрощенный способ пересчета координат дает достаточную точность.
Теперь перейдем от глобуса к бумажной карте. Как получилось выпуклую поверхность Земли разместить на плоской карте?
Для того чтобы понять насколько это непростая задача, попробуйте аккуратно срезать часть кожицы апельсина, положить ее на стол и придавить, чтобы сделать плоской. Кожица, скорее всего, лопнет, наводя нас на мысль, что создание плоских карт выпуклой поверхности совсем нетривиальная задача. Процесс расплющивания апельсиновой шкурки, по-умному, называется переходом от сферической системы координат (эллипсоида) к плоской (карте). И выполняется это при помощи проектирования.
Тут надо вспомнить основы черчения. Проекция – это представление объемной фигуры на плоскости. В нашем случае, такой фигурой является земная поверхность. Разновидностей проекций много, но классифицируются они обычно по своим свойствам сохранять углы и/или расстояния при проектировании. Тень – простейший пример проекции освещаемого предмета на плоскость. Важно запомнить, что любая проекция вносит искажения в форму геометрической фигуры, либо съедает большую часть информации о ней. Например, если осветить спичечный коробок фонариком, то по его тени мы не сможем восстановить истинную форму освещаемого объекта – коробка.
Картографические проекции – это способ представления земной поверхности на плоской карте. Самая известная и часто используемая картографическая проекция – поперечно-цилиндрическая. Чтобы представить себе как получается данная проекция надо включить пространственное воображение. Возьмем, мысленно, цилиндр и шарик одинакового диаметра. Шарик - это наша планета. Для упрощения представим, что ось ее вращения направлена вертикально вверх. В таком положении поместим шарик внутрь горизонтально расположенного цилиндра. Шарик будет соприкасаться с цилиндром по меридиану (вертикальная линия). Теперь спроектируем наш шарик на поверхность цилиндра. Если непонятно как это сделать, представьте себе пучок параллельных лучей пронзающих шарик и переносящих его изображение на цилиндр, на поверхности цилиндра получается как бы фотография шарика. Затем цилиндр разрежем вдоль и развернем – мы получили представление нашего шарика на плоскости – его проекцию (рис.1).

Рис. 1. Поперечно-цилиндрическая проекция
В картографии получили распространение две разновидности поперечно-цилиндрической проекции:
1. Проекция Гаусса-Крюгера (на территории бывшего СССР).
2. UTM – универсальная поперечная проекция Меркатора (во всем мире).
Разница между этими двумя проекциями совсем незначительная. То, что мы с вами представляли - это и была проекция Гаусса-Крюгера , в ней наш воображаемый шарик соприкасался с цилиндром в одном месте. В проекции UTM не удалось найти шарик одинакового с цилиндром диаметра, шарик оказался больше и пересекался цилиндром в двух местах :). Это конечно шутка. На самом деле такой вид проекции придуман, чтобы уменьшить искажения, о чем мы поговорим немного позже.
Если вам интересно, что означает слово Меркатор из аббревиатуры UTM, то скажу что это фамилия нидерландского картографа, который, как считается, впервые применил этот вид проекции еще в 16 веке при создании карты мира.
Я уже упоминал, что любая проекция либо съедает большую часть информации о форме проектируемого предмета, либо вносит искажения его формы (либо и то и другое). Рассмотренная поперечно-цилиндрическая проекция не искажает углы, а лишь искажает расстояния. Причем истинные расстояния будут только в местах соприкосновения цилиндра и нашего воображаемого шарика. В остальных областях расстояния искажаются. Величина искажений расстояний задается масштабным коэффициентом – числом, на которое надо умножить длину спроектированного отрезка для получения истинной его длины.
Проекции Гаусса-Крюгера и UTM делят земной эллипсоид на зоны. Зона – это область, участвующая в проектировании. То есть одна зона – это одна проекция. И в UTM и в проекции Гаусса-Крюгера используются зоны в 6°. Проведя несложные расчеты: 360°/6°=60, получаем необходимое количество зон, чтобы спроектировать на плоскость весь земной эллипсоид. Центральный меридиан каждой зоны называют также осевым меридианом. Зоны нумеруются с запада на восток, от Гринвича для проекции Гаусса-Крюгера и от -180° для UTM. Для проекции Гаусса-Крюгера меридианы 0° и 6° определяют границы первой зоны, осевой меридиан - 3°, 6° и 12° - границы второй зоны, осевой меридиан - 9° и т.д. пока не будет разделен весь эллипсоид.
Почему используются именно зоны в 6°? Точного ответа я не знаю, но думаю, что такая ширина зон выбрана, во-первых, для удобства разбивки (360 делится на 6 без остатка и центральные меридианы – тоже всегда целое число) и, во-вторых, ширина зоны оказывается не слишком большой (не вносятся большие искажения при проектировании, которые для проекции Гаусса-Крюгера максимальны на границах зоны, а для UTM еще велики и возле центрального меридиана, но абсолютная величина искажений при этом в пределах зоны меньше чем в проекции Гаусса-Крюгера).
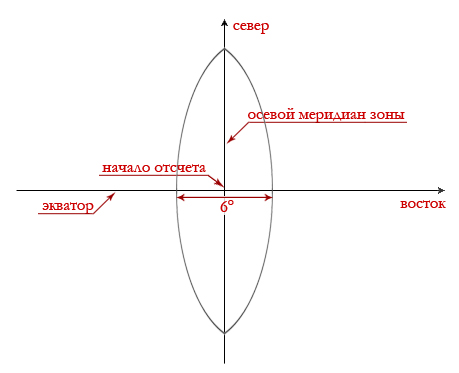
Рис. 2. 6-ти градусная зона проекции UTM или Гаусса-Крюгера
После проектирования зоны на плоскость мы получаем лепесток, контур которого – это меридианы – границы зоны. Теперь необходимо перейти к какой-то системе координат на плоскости. Иначе, зачем мы все это затеяли? Началом отсчета такой системы координат была выбрана точка пересечения центрального меридиана зоны с экватором. Зона покрывается километровой сеткой – расчерчивается вертикальными и горизонтальными линиями, которые параллельны, соответственно, центральному меридиану и экватору. Вот тут кроется подвох. Многие заблуждаются, полагая, что вертикальные линии километровой сетки ориентированы строго на север. Это не так. Надеюсь, вы понимаете почему? Не буду снова объяснять особенности поперечно-цилиндрической проекции, просто взгляните на меридианы – границы зоны, они и есть - линии направленные строго на север. То есть единственная линия километровой сетки, ориентированная строго на север, для проекции Гаусса-Крюгера находится в начале отсчета – это центральный меридиан зоны.
Итак, начало отсчета этих проекций – это центр зоны. Но это точка не имеет координат 0,0. Вводится так называемое смещение – добавочные величины, которые исключают отрицательные значения координат в пределах зоны. Центру зоны назначили координаты 10 000 км (смещение на север) и 500 км (смещение на восток).
Мы с вами произвели важное действие – перешли от сферической системы координат (широта, долгота на земном эллипсоиде) к плоской (метры в прямоугольной системе координат). При этом поменялся центр системы – начало отсчета координат. Как мы помним, в сферической системе координат, использующей земной эллипсоид за начало отсчета принимается центр этого эллипсоида – это геоцентрическая система. Плоские же системы координат называют топоцентрическими, их начало отсчета находится в плоскости проекции.
Теперь, надеюсь, понимая основы используемых в картографии и геодезии систем координат и проекций, перейдем к пересчету координат из одной системы в другую.